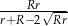Zadanie nr 3697665
Dwa okręgi o promieniach  i
i 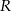 (
(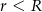 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 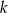 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 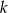 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
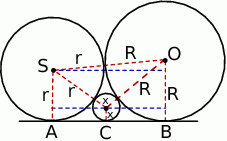
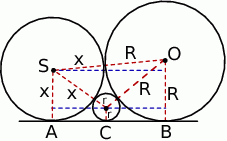
Na razie nie przejmujmy się drugim przypadkiem (zresztą nie bardzo widać jak miałby wyglądać). Oznaczmy szukaną długość promienia przez  . Wyliczymy długość odcinka
. Wyliczymy długość odcinka  na dwa sposoby, co pozwoli nam uzyskać zależność między
na dwa sposoby, co pozwoli nam uzyskać zależność między  i
i 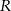 . Z jednej strony
. Z jednej strony
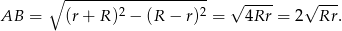
Z drugiej strony
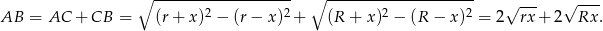
Mamy stąd
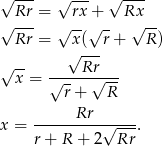
Pora teraz zastanowić się jak wygląda drugi przypadek. Aby to sobie wyobrazić popatrzmy jeszcze raz na poprzedni rysunek, ale wyobraźmy sobie, że tym razem dane są okręgi o promieniach  i
i 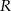 . Innymi słowy, oprócz okręgu ’pomiędzy’ danymi okręgami jest jeszcze jeden, który jest ’na zewnątrz’.
. Innymi słowy, oprócz okręgu ’pomiędzy’ danymi okręgami jest jeszcze jeden, który jest ’na zewnątrz’.
Rachunkowo mamy dokładnie tę samą sytuację, ale musimy zamienić rolami  i
i  . Mamy zatem
. Mamy zatem
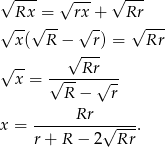
Odpowiedź: 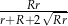 lub
lub