/Konkursy/Zadania/Geometria/Planimetria/Okrąg i koło/Styczne

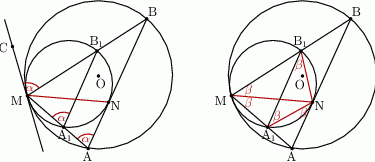
Zadanie nr 6492001

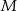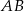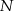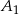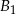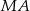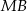Dwa okręgi są styczne wewnętrznie w punkcie M . Cięciwa AB większego okręgu jest styczna do mniejszego okręgu w punkcie N . Oznaczmy przez A 1 i B1 punkty przecięcia prostych MA i MB z mniejszym okręgiem. Udowodnić, że

  • prosta 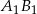A 1B1 jest równoległa do prostej AB ;
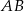  • prosta 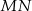MN jest dwusieczną kąta AMB .
Wersja PDF

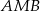Rozwiązanie

  • Dorysujmy wspólną styczną 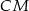CM obu okręgów i oznaczmy ∡CMB = α .
    PIC

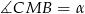    W takim razie patrząc na mniejszy okrąg i korzystając z twierdzenia o stycznej i siecznej, otrzymujemy

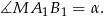
    ∡MA 1B 1 = α.

    Jeżeli natomiast popatrzymy na cięciwę 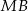MB większego okręgu to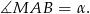

    ∡MAB = α.

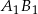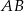    To oznacza, że proste A 1B 1 i AB przecinają prostą 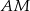AM pod tym samym kątem, czyli są równoległe.

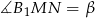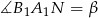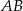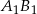  • Teraz oznaczmy ∡B 1MN = β . W takim razie ∡B 1A 1N = β (bo są oparte na tym samym łuku). Teraz korzystamy z poprzedniego podpunktu, czyli z tego, że proste AB i A 1B1 są równoległe. Mamy stąd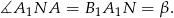
    ∡A NA = B A N = β. 1 1 1

    Teraz ponownie korzystamy z twierdzenia o stycznej i siecznej i mamy

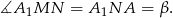
    ∡A 1MN = A 1NA = β .

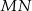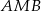    Zatem istotnie prosta MN jest dwusieczną kąta AMB .

Wersja PDF