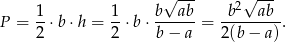Zadanie nr 4844401
Na ramionach 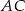 i
i 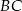 trójkąta równoramiennego
trójkąta równoramiennego 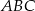 wybrano punkty
wybrano punkty 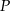 i
i 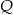 w ten sposób, że odcinek
w ten sposób, że odcinek 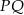 jest równoległy do podstawy
jest równoległy do podstawy 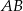 i styczny do okręgu wpisanego w trójkąt
i styczny do okręgu wpisanego w trójkąt 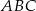 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 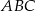 jest równe
jest równe
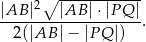
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
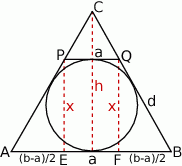
Oznaczmy 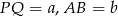 . Zauważmy, że trapez równoramienny
. Zauważmy, że trapez równoramienny 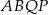 jest opisany na okręgu, więc łatwo obliczyć długość jego ramienia.
jest opisany na okręgu, więc łatwo obliczyć długość jego ramienia.
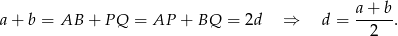
Teraz z trójkąta prostokątnego 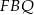 łatwo obliczyć odległość
łatwo obliczyć odległość  między prostymi
między prostymi 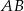 i
i 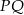 (czyli wysokość trapezu
(czyli wysokość trapezu 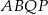 ).
).
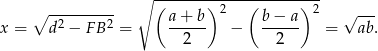
Aby teraz obliczyć wysokość 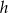 trójkąta
trójkąta 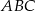 korzystamy z podobieństwa trójkątów
korzystamy z podobieństwa trójkątów 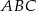 i
i 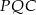 .
.
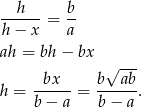
Pole trójkąta  jest więc równe
jest więc równe