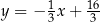Zadanie nr 1908148
Kwadrat 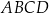 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 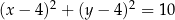 oraz
oraz 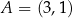 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 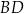 tego kwadratu.
tego kwadratu.
Rozwiązanie
Dany okrąg to okrąg o środku 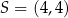 i przechodzący przez punkt
i przechodzący przez punkt 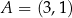 (o promieniu
(o promieniu 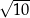 ). To pozwala wykonać szkicowy rysunek.
). To pozwala wykonać szkicowy rysunek.
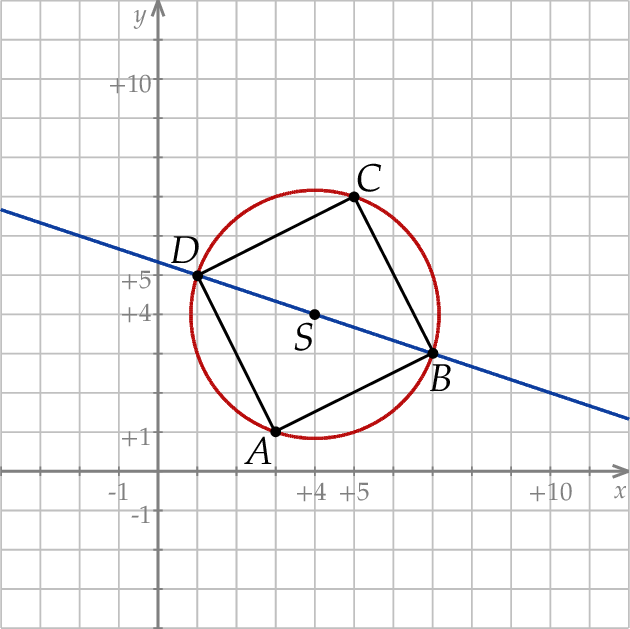
Zauważmy, że szukana prosta 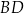 to prosta prostopadła do prostej
to prosta prostopadła do prostej 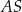 i przechodząca przez
i przechodząca przez 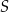 (bo przekątne kwadratu są prostopadłe).
(bo przekątne kwadratu są prostopadłe).
Sposób I
Rozpocznijmy od napisania równania prostej 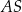 – szukamy prostej w postaci
– szukamy prostej w postaci 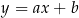 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów 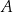 i
i 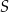 mamy
mamy
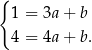
Odejmując od drugiego równania pierwsze (żeby skrócić 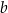 ) mamy
) mamy 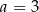 . Współczynnika
. Współczynnika 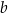 możemy nie obliczać, bo nie jest nam do niczego potrzebny.
możemy nie obliczać, bo nie jest nam do niczego potrzebny.
Szukana prosta 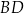 jest prostopadła do
jest prostopadła do 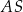 , więc ma równanie postaci
, więc ma równanie postaci 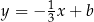 . Współczynnik
. Współczynnik 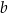 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 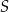 .
.
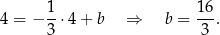
Zatem szukana prosta ma równanie 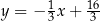
Sposób II
Równanie prostej 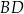 można łatwo napisać jeżeli skorzystamy ze wzoru na równanie prostej prostopadłej do wektora
można łatwo napisać jeżeli skorzystamy ze wzoru na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/1908148/HzadR23x.png) i przechodzącej przez punkt
i przechodzącej przez punkt 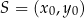
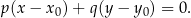
W naszej sytuacji mamy 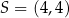 i
i
![−→ →v = AS = [4− 3,4− 1] = [1,3].](https://img.zadania.info/zad/1908148/HzadR27x.png)
Prosta 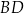 ma więc równanie
ma więc równanie
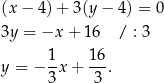
Odpowiedź: