/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt/Kwadrat

Zadanie nr 9843171

Wyznacz współrzędne środka okręgu opisanego na kwadracie, którego jeden z boków jest zawarty w prostej o równaniu 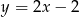y = 2x − 2 , a punkt 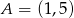A = (1,5) jest jego wierzchołkiem. Rozważ wszystkie przypadki.

Wersja PDF

Rozwiązanie

Aby wyznaczyć wierzchołek 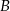B , napiszmy równanie prostej prostopadłej do danej prostej 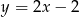y = 2x − 2 i przechodzącej przez punkt A .

PIC

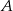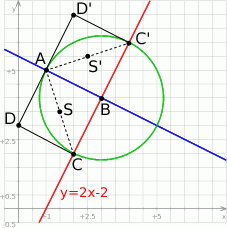
Prosta ta jest postaci 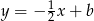y = − 12x + b oraz przechodzi przez punkt 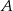A , więc

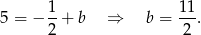
5 = − 1+ b ⇒ b = 11. 2 2

Znajdujemy punkt wspólny 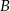B obu prostych

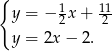
{ y = − 12 x+ 121 y = 2x − 2.

Odejmujemy od drugiego równania pierwsze (żeby skrócić 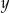y ) i mamy

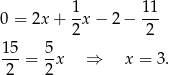
1 11 0 = 2x + --x− 2− --- 2 2 15-= 5x ⇒ x = 3. 2 2

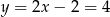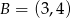Stąd y = 2x − 2 = 4 i B = (3,4) . Długość boku kwadratu wynosi

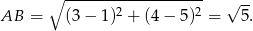
∘ ------------------- √ -- AB = (3− 1 )2 + (4 − 5)2 = 5.

Aby znaleźć kolejny wierzchołek szukamy na prostej 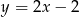y = 2x − 2 punktu 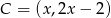C = (x,2x − 2 ) odległego od 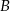B o √ -- 5 .

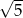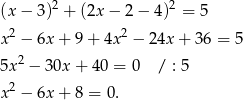
(x − 3 )2 + (2x − 2 − 4 )2 = 5 2 2 x − 6x + 9+ 4x − 24x + 36 = 5 5x 2 − 3 0x+ 40 = 0 / : 5 2 x − 6x + 8 = 0.

Rozwiązujemy otrzymane równanie kwadratowe.

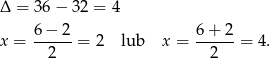
Δ = 36 − 32 = 4 6 − 2 6 + 2 x = --2---= 2 lub x = --2---= 4.

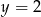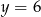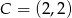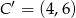Wtedy odpowiednio y = 2 lub y = 6 . Mamy więc dwie możliwości: C = (2,2) lub ′ C = (4,6) . Liczymy współrzędne środka przekątnej 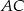AC w każdym z tych przypadków.

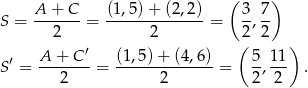
A + C (1 ,5)+ (2 ,2) ( 3 7) S = -------= -------------- = -, -- 2 2 (2 2 ) ′ A + C′ (1,5)+ (4,6) 5 11 S = ------- = --------------= --,--- . 2 2 2 2

 
Odpowiedź: 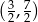(3 7) 2,2 lub (5 11) 2,-2

Wersja PDF