/Szkoła średnia/Nierówności/Wymierne/Z parametrem

Zadanie nr 1243734

Dodaj do ulubionych
Dodaj do rozwiązanych

Wiedząc, że przedział 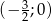3 (− 2;0) jest zbiorem wszystkich rozwiązań nierówności 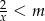x2< m z niewiadomą x , oblicz m .

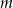Rozwiązanie

Sposób I

Narysujmy wykres funkcji 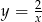2 y = x .

PIC

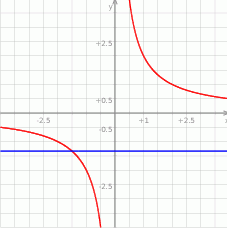
Łatwo sprawdzić, że 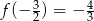3 4 f (− 2) = − 3 . Zatem wykres funkcji 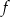f jest poniżej prostej 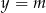y = m dokładnie na przedziale 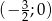3 (− 2;0) tylko dla 4 m = − 3 .

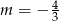Sposób II

Rozwiążmy podaną nierówność

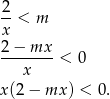
2 --< m x 2−--mx--< 0 x x (2− mx ) < 0.

Aby rozwiązaniem tej nierówności był jeden ograniczony przedział, musi to być parabola o ramionach skierowanych w górę, czyli 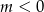m < 0 . Ponadto miejscami zerowymi tej paraboli muszą być liczby 0 i 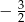3 − 2 . Stąd

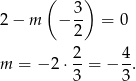
( ) 2− m − 3- = 0 2 2 4 m = − 2⋅ --= − --. 3 3

 
Odpowiedź: 4 m = − 3

Wersja PDF