Zadanie nr 7712600
Znajdź takie wartości parametru 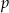 , aby zbiorem rozwiązań nierówności
, aby zbiorem rozwiązań nierówności 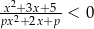 był zbiór liczb rzeczywistych.
był zbiór liczb rzeczywistych.
Rozwiązanie
Zauważmy, że licznik jest zawsze dodatni (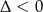 ), więc pozostaje nam nierówność
), więc pozostaje nam nierówność
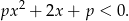
Aby nierówność ta była zawsze prawdziwa musi być 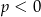 (należy też sprawdzić co się dzieje dla
(należy też sprawdzić co się dzieje dla 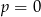 !) i
!) i 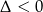 , czyli
, czyli
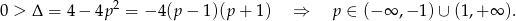
W połączeniu z warunkiem 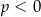 mamy
mamy 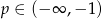 .
.
Odpowiedź: