Zadanie nr 1838865
W trójkącie równoramiennym dane są długości podstawy 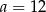 cm i wysokości
cm i wysokości 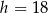 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.
Rozwiązanie
Zaczynamy oczywiście od rysunku.
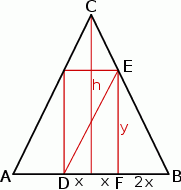
Oznaczmy boki prostokąta przez 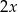 i
i 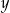 – jak na rysunku. Ponieważ przekątna
– jak na rysunku. Ponieważ przekątna 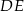 jest równoległa do boku
jest równoległa do boku 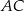 , to trójkąt
, to trójkąt 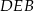 jest równoramienny, zatem jego wysokość opuszczona z wierzchołka
jest równoramienny, zatem jego wysokość opuszczona z wierzchołka 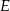 dzieli podstawę
dzieli podstawę 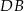 na dwa równe odcinki, każdy z nich ma więc długość
na dwa równe odcinki, każdy z nich ma więc długość 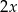 . W takim razie
. W takim razie 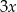 to połowa podstawy trójkąta
to połowa podstawy trójkąta 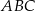 , czyli
, czyli 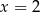 .
.
Bok 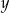 możemy wyliczyć z podobieństwa trójkątów
możemy wyliczyć z podobieństwa trójkątów 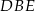 i
i 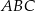 .
.
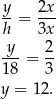
Drugi bok ma długość 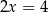 .
.
Odpowiedź: 4 cm i 12 cm.

