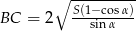/Konkursy/Zadania/Geometria/Planimetria/Trójkąt/Różne

Zadanie nr 8980481

Dodaj do ulubionych
Dodaj do rozwiązanych

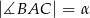Oblicz jaka może być najmniejsza możliwa długość boku BC trójkąta ABC jeżeli |∡BAC | = α i pole trójkąta 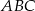ABC jest równe S .

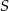Rozwiązanie

Szkicujemy trójkąt.

PIC

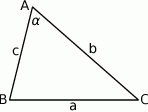
Zauważmy, że jeżeli ustalony jest kąt 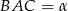BAC = α i pole

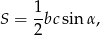
S = 1bc sin α, 2

to stałą wartość ma też iloczyn

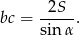
2S bc = -----. sinα

Długość boku 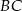BC możemy obliczyć z twierdzenia cosinusów

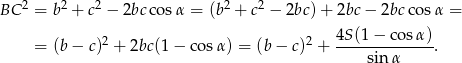
BC 2 = b2 + c2 − 2bc cosα = (b2 + c2 − 2bc )+ 2bc − 2bccos α = 2 2 4S-(1−--cosα-) = (b− c) + 2bc(1 − co sα) = (b − c) + sin α .

Zauważmy teraz, że drugi składnik tej sumy jest stały, więc najmniejszą możliwą długość 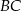BC otrzymamy gdy 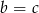b = c . Wtedy

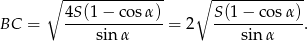
∘ -------------- ∘ ------------- BC = 4S(1-−-cos-α)-= 2 S(1-−-co-sα). sinα sinα

 
Odpowiedź: ∘ --------- BC = 2 S(1−cosα) sinα

Wersja PDF