Zadanie nr 2091404
Wykaż, że jeżeli  i
i 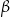 są kątami trójkąta oraz
są kątami trójkąta oraz 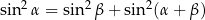 to trójkąt ten jest prostokątny.
to trójkąt ten jest prostokątny.
Rozwiązanie
Narysujmy sobie taki trójkąt.
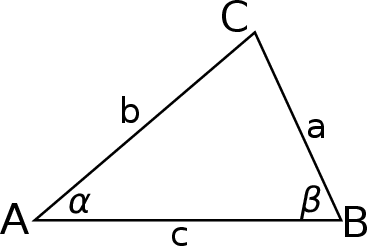
Sposób I
Zauważmy, że
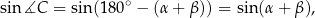
czyli na mocy twierdzenia sinusów mamy
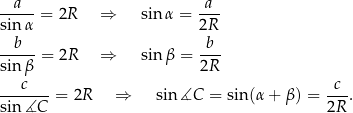
Zatem podany w treści warunek możemy zapisać w postaci
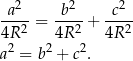
Zatem trójkąt jest prostokątny.
Sposób II
Tym razem pozostaniemy w krainie trygonometrii. Na mocy wzoru
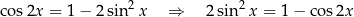
łatwo się pozbyć kwadratów w wyjściowej równości.
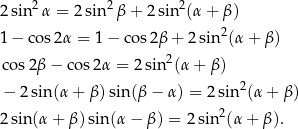
Skorzystaliśmy oczywiście ze wzoru na różnicę cosinusów. Ponieważ 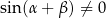 daje to nam
daje to nam
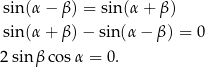
Tym razem skorzystaliśmy ze wzoru na różnicę sinusów. Ponieważ 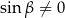 daje to nam
daje to nam