Zadanie nr 3515923
Na bokach 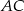 i
i 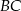 trójkąta
trójkąta 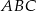 obrano punkty
obrano punkty 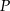 i
i 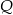 takie, że
takie, że 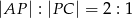 oraz
oraz 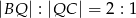 . Odcinki
. Odcinki 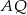 i
i 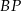 przecinają się w punkcie
przecinają się w punkcie 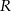 . Wykaż, że pole czworokąta
. Wykaż, że pole czworokąta 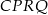 jest równe polu trójkąta
jest równe polu trójkąta 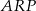 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
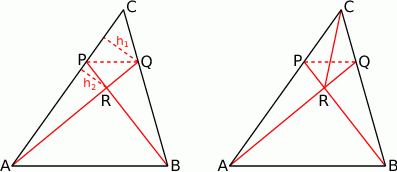
Sposób I
Zauważmy, że wystarczy wykazać, że pole trójkąta 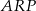 stanowi połowę pola trójkąta
stanowi połowę pola trójkąta 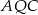 . Wiemy jaki jest stosunek podstaw tych trójkątów:
. Wiemy jaki jest stosunek podstaw tych trójkątów: 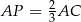 , pozostało ustalić stosunek ich wysokości
, pozostało ustalić stosunek ich wysokości 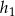 i
i 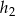 .
.
Zauważmy najpierw, że na mocy twierdzenia Talesa
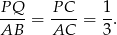
Zauważmy ponadto, że trójkąty 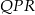 i
i 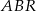 są podobne (mają równe kąty) i obliczony wyżej iloraz jest ich skalą podobieństwa. Stąd
są podobne (mają równe kąty) i obliczony wyżej iloraz jest ich skalą podobieństwa. Stąd 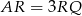 oraz
oraz
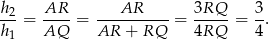
To oznacza, że
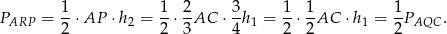
Stąd
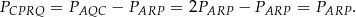
Sposób II
Tym razem dorysujmy odcinek 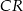 . Zauważmy, że trójkąty
. Zauważmy, że trójkąty 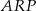 i
i 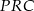 mają wspólną wysokość opuszczoną na prostą
mają wspólną wysokość opuszczoną na prostą 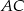 , a stosunek długości podstaw tych trójkątów odpowiadających tej wysokości jest równy 2:1. Stąd
, a stosunek długości podstaw tych trójkątów odpowiadających tej wysokości jest równy 2:1. Stąd
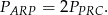
Podobnie, patrząc na trójkąty 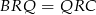 , uzasadniamy
, uzasadniamy
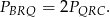
Mamy stąd
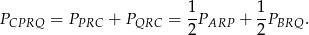
Wystarczy teraz wykazać, że 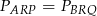 .
.
Zauważmy, że trójkąty 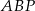 i
i 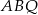 mają wspólną podstawę
mają wspólną podstawę 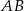 oraz równe wysokości opuszczone na tę podstawę. Trójkąty te mają więc równe pola. To oznacza, że
oraz równe wysokości opuszczone na tę podstawę. Trójkąty te mają więc równe pola. To oznacza, że
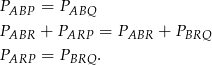
To oznacza, że