Zadanie nr 3559487
W trójkąt 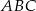 , w którym
, w którym 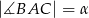 oraz
oraz 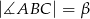 , wpisano okrąg. Punkty
, wpisano okrąg. Punkty 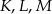 są punktami styczności okręgu odpowiednio z bokami
są punktami styczności okręgu odpowiednio z bokami 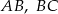 i
i 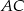 . Wykaż, że
. Wykaż, że 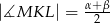 .
.
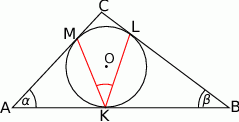
Rozwiązanie
Sposób I
Jeżeli połączymy środek okręgu wpisanego z punktami styczności, otrzymamy odcinki 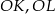 i
i 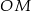 , które są prostopadłe do odpowiednich boków trójkąta.
, które są prostopadłe do odpowiednich boków trójkąta.
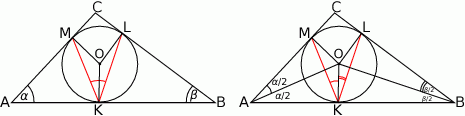
Zauważmy ponadto, że kąty 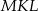 i
i 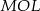 są opisane na tym samym łuku okręgu wpisanego w trójkąt
są opisane na tym samym łuku okręgu wpisanego w trójkąt 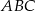 . Zatem
. Zatem
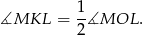
Patrzymy teraz na czworokąt 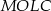 .
.
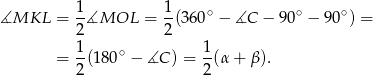
Sposób II
Tak jak poprzednio zauważamy, że
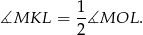
Ponieważ suma kątów czworokąta jest równa 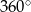 , patrząc na czworokąty
, patrząc na czworokąty 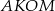 i
i 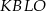 mamy
mamy
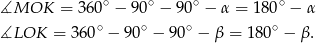
Ponadto
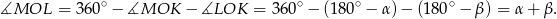
Zatem
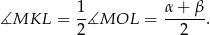
Sposób III
Zauważmy, że w czworokątach 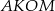 i
i 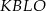 sumy dwóch przeciwległych kątów są równe
sumy dwóch przeciwległych kątów są równe 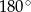 , co oznacza, że na każdym z tych czworokątów można opisać okrąg. W takim razie kąty
, co oznacza, że na każdym z tych czworokątów można opisać okrąg. W takim razie kąty 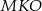 oraz
oraz 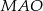 są kątami wpisanymi w pewien okrąg i są oparte na tym samym łuku
są kątami wpisanymi w pewien okrąg i są oparte na tym samym łuku 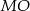 . Zatem
. Zatem
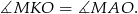
Podobnie
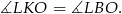
Teraz pozostało zauważyć, że proste 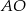 i
i 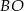 są dwusiecznymi odpowiednio kątów
są dwusiecznymi odpowiednio kątów 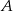 i
i 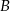 trójkąta (bo środek okręgu wpisanego to punkt przecięcia się dwusiecznych). Zatem
trójkąta (bo środek okręgu wpisanego to punkt przecięcia się dwusiecznych). Zatem
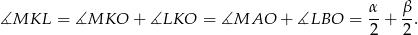
Sposób IV
Zauważmy, że trójkąt 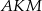 jest równoramienny (bo trójkąty
jest równoramienny (bo trójkąty 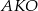 i
i  są przystające). W takim razie
są przystające). W takim razie
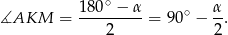
Analogicznie
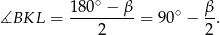
Mamy zatem