Zadanie nr 4043117
Miary kątów trójkąta 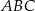 są równe
są równe 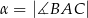 ,
, 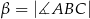 i
i 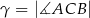 . Punkt
. Punkt 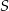 jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki
jest środkiem okręgu wpisanego w ten trójkąt, a proste zawierające odcinki 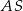 i
i 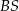 przecinają boki
przecinają boki 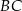 i
i 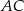 tego trójkąta w punktach odpowiednio
tego trójkąta w punktach odpowiednio 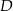 i
i 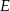 (zobacz rysunek).
(zobacz rysunek).
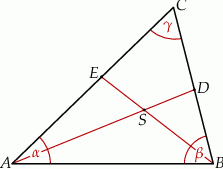
Wykaż, że jeżeli 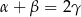 , to na czworokącie
, to na czworokącie 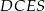 można opisać okrąg.
można opisać okrąg.
Rozwiązanie
Zauważmy, że
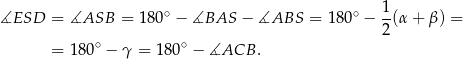
To oznacza, że suma dwóch przeciwległych kątów czworokąta 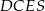 jest równa
jest równa 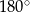 , więc rzeczywiście na czworokącie tym można opisać okrąg.
, więc rzeczywiście na czworokącie tym można opisać okrąg.

