/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij...

Zadanie nr 4372297

Dodaj do ulubionych
Dodaj do rozwiązanych

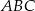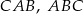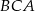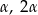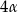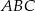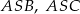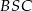Trójkąt ABC jest wpisany w okrąg o środku S . Kąty wewnętrzne CAB , ABC i BCA tego trójkąta są równe, odpowiednio, α, 2α i 4α . Wykaż, że trójkąt ABC jest rozwartokątny, i udowodnij, że miary wypukłych kątów środkowych ASB , ASC i BSC tworzą w podanej kolejności ciąg arytmetyczny.

Rozwiązanie

Suma kątów w trójkącie jest równa 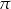π , więc

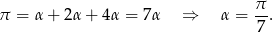
π- π = α + 2α + 4 α = 7α ⇒ α = 7 .

W takim razie 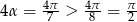4α = 4π-> 4π-= π- 7 8 2 , co oznacza, że kąt przy wierzchołku 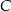C jest rozwarty.

Możemy teraz naszkicować opisaną sytuację – trzeba przy tym odrobinę uważać; ponieważ trójkąt jest rozwartokątny środek okręgu znajduje się na zewnątrz trójkąta.

PIC

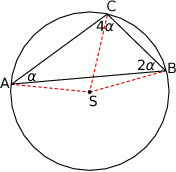
Miary kątów środkowych obliczamy z twierdzenia o kątach wpisanym i środkowym.

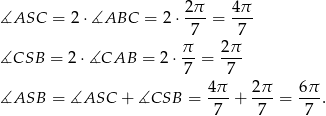
∡ASC = 2 ⋅∡ABC = 2 ⋅ 2π = 4-π 7 7 π 2π ∡CSB = 2 ⋅∡CAB = 2⋅ 7-= -7- ∡ASB = ∡ASC + ∡CSB = 4π- + 2π- = 6π-. 7 7 7

Otrzymany ciąg kątów

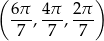
( 6π 4π 2π ) ---, ---,--- 7 7 7

jest oczywiście arytmetyczny (z różnicą 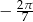2π − 7-- ).

Wersja PDF