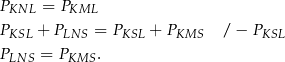Zadanie nr 4868105
Punkty 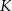 i
i 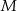 oraz
oraz 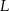 i
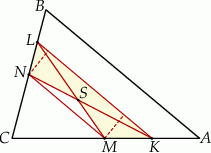
i 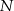 dzielą odpowiednio boki
dzielą odpowiednio boki 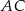 i
i 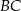 trójkąta
trójkąta 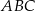 w stosunku
w stosunku 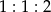 (zobacz rysunek). Odcinki
(zobacz rysunek). Odcinki 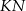 i
i 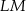 przecinają się w punkcie
przecinają się w punkcie 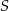 .
.
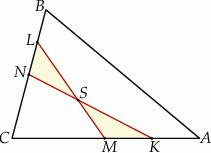
Uzasadnij, że pola trójkątów 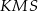 i
i 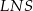 są równe.
są równe.
Rozwiązanie
Dorysujmy odcinki 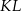 i
i 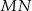 .
.
Trójkąty 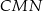 ,
, 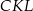 i
i 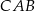 mają wspólny kąt przy wierzchołku
mają wspólny kąt przy wierzchołku 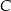 oraz proporcjonalne boki wychodzące z tego wierzchołka. Zatem każde dwa z nich są do siebie podobne. W szczególności
oraz proporcjonalne boki wychodzące z tego wierzchołka. Zatem każde dwa z nich są do siebie podobne. W szczególności 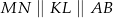 , czyli czworokąt
, czyli czworokąt 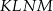 jest trapezem (mogliśmy też to uzasadnić korzystając z twierdzenia Talesa). To z kolei oznacza, że trójkąty
jest trapezem (mogliśmy też to uzasadnić korzystając z twierdzenia Talesa). To z kolei oznacza, że trójkąty 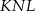 i
i 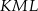 mają wspólną podstawę
mają wspólną podstawę 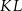 oraz równe wysokości opuszczone na tę podstawę. Zatem
oraz równe wysokości opuszczone na tę podstawę. Zatem