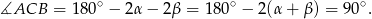/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij...

Zadanie nr 7156705

Dodaj do ulubionych
Dodaj do rozwiązanych

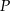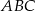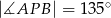Punkt P jest środkiem okręgu wpisanego w trójkąt ABC oraz ∘ |∡AP B | = 135 . Wykaż, że trójkąt 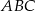ABC jest prostokątny.

Rozwiązanie

Robimy rysunek.

PIC

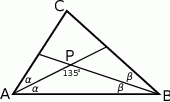
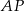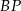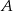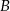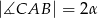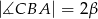Ponieważ środek okręgu wpisanego jest punktem przecięcia się dwusiecznych, odcinki AP i BP dzielą kąty przy wierzchołkach A i B na połowy. Jeżeli oznaczymy |∡CAB | = 2α i |∡CBA | = 2β to mamy

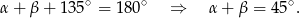
∘ ∘ ∘ α + β+ 135 = 18 0 ⇒ α + β = 45 .

Mamy zatem

∘ ∘ ∘ ∡ACB = 1 80 − 2α− 2β = 180 − 2(α + β) = 9 0 .
Wersja PDF