Zadanie nr 8590575
W trójkącie 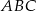 dwusieczna kąta
dwusieczna kąta 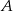 przecina bok
przecina bok 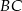 w punkcie
w punkcie 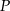 . Przez punkt
. Przez punkt 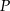 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 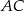 , przecinającą bok
, przecinającą bok 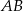 w punkcie
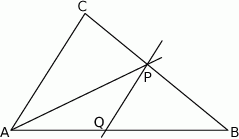
w punkcie 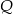 (rys.). Udowodnij, że
(rys.). Udowodnij, że 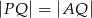 .
.
Rozwiązanie
Prosta 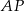 jest dwusieczną kąta
jest dwusieczną kąta 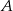 , więc
, więc
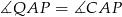
wiemy też, że prosta 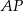 przecina proste równoległe
przecina proste równoległe 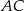 i
i 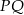 pod tym samym kątem, więc
pod tym samym kątem, więc
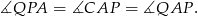
To oznacza, że trójkąt 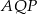 jest równoramienny, więc rzeczywiście
jest równoramienny, więc rzeczywiście 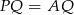 .
.

