/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Udowodnij...

Zadanie nr 8684602

Dodaj do ulubionych
Dodaj do rozwiązanych

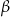Wykaż, że jeśli α i β są kątami trójkąta oraz 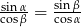sin-α sinβ cosβ = cosα to trójkąt ten jest równoramienny lub prostokątny.

Rozwiązanie

Przekształcimy podaną równość korzystając ze wzoru

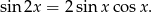
sin 2x = 2 sinx cos x.

Liczymy

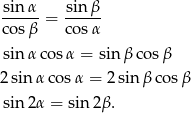
sin α sin β ----- = ----- cos β cosα sin αco sα = sin βco sβ 2sin αco sα = 2 sinβ cos β sin 2α = sin 2β.

Sposób I

Ponieważ 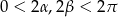0 < 2α,2β < 2π , powyższa równość oznacza, że 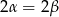2α = 2β – wtedy trójkąt jest równoramienny, lub 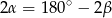2α = 180∘ − 2β . W tym drugim przypadku mamy 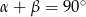α + β = 90∘ , czyli trzeci kąt trójkąta jest prosty.

Sposób II

Możemy też skorzystać ze wzoru na różnicę sinusów

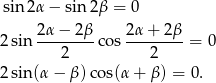
sin 2α − sin2 β = 0 2α-−--2β 2-α+--2β 2 sin 2 cos 2 = 0 2 sin (α− β)co s(α+ β) = 0.

Zatem albo 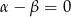α − β = 0 , co oznacza, że trójkąt jest równoramienny, albo 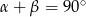∘ α + β = 90 , co oznacza, że trójkąt jest prostokątny.

Wersja PDF