Zadanie nr 9215423
Na bokach 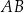 i
i 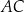 trójkąta
trójkąta 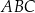 wybrano odpowiednio punkty
wybrano odpowiednio punkty 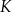 i
i 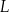 w ten sposób, że
w ten sposób, że 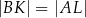 . Punkt
. Punkt 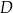 jest środkiem odcinka
jest środkiem odcinka 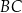 . Przez punkty
. Przez punkty 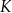 i
i 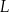 poprowadzono proste równoległe do
poprowadzono proste równoległe do 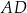 , które wyznaczyły na boku
, które wyznaczyły na boku 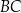 punkty
punkty 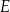 i
i 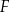 odpowiednio (zobacz rysunek). Wykaż, że jeżeli
odpowiednio (zobacz rysunek). Wykaż, że jeżeli 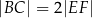 , to
, to 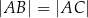 .
.

Rozwiązanie
Oznaczmy 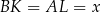 ,
, 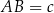 ,
, 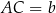 ,
, 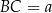 .
.
Zauważmy, że trójkąt 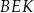 jest podobny do trójkąta
jest podobny do trójkąta 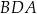 w skali
w skali 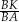 , więc
, więc
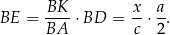
Podobnie, z podobieństwa trójkątów 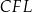 i
i 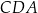 mamy
mamy
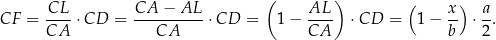
Stąd