Zadanie nr 5278691
Uporządkuj rosnąco liczby 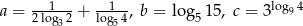 .
.
Rozwiązanie
Liczymy
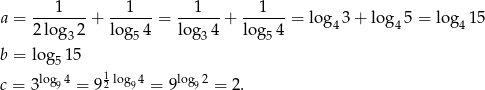
Jest jasne, że
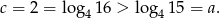
Aby porównać liczby  i
i 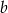 zmieńmy w obu podstawę na 15.
zmieńmy w obu podstawę na 15.
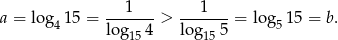
Odpowiedź: 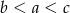
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Uporządkuj rosnąco liczby 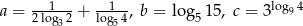 .
.
Liczymy
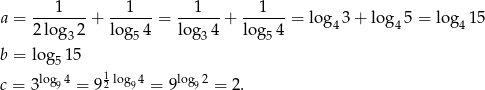
Jest jasne, że
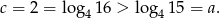
Aby porównać liczby  i
i 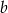 zmieńmy w obu podstawę na 15.
zmieńmy w obu podstawę na 15.
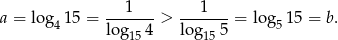
Odpowiedź: