Zadanie nr 8583428
Dany jest prostokąt 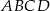 , w którym
, w którym 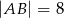 i
i 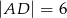 . Na boku
. Na boku 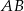 zbudowano trójkąt równoboczny
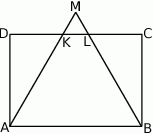
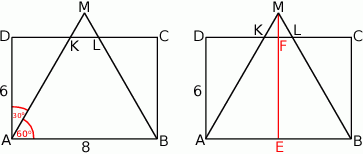
zbudowano trójkąt równoboczny 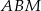 (patrz rysunek). Oblicz obwód trójkąta
(patrz rysunek). Oblicz obwód trójkąta 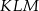 .
.
Rozwiązanie
Sposób I
Wiemy, że kąty trójkąta równobocznego mają miarę 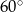 .
.
W takim razie
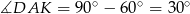
i mamy
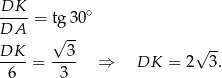
To z kolei oznacza, że
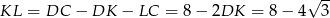
i obwód trójkąta równobocznego 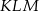 jest równy
jest równy
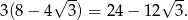
Sposób II
Jeżeli nie chcemy korzystać z trygonometrii dorysujmy wysokość trójkąta 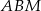 . Ponieważ
. Ponieważ 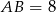 mamy
mamy
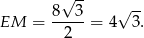
Zatem
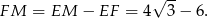
Jeżeli teraz oznaczymy 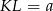 to mamy równanie
to mamy równanie
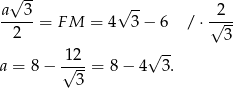
Zatem obwód trójkąta 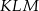 jest równy
jest równy
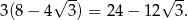
Odpowiedź: 

