Zadanie nr 2087081
Punkt 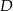 jest środkiem boku
jest środkiem boku 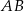 trójkąta
trójkąta 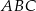 , w którym
, w którym 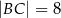 ,
, 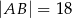 i
i 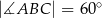 . Oblicz pole trójkąta
. Oblicz pole trójkąta 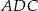 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
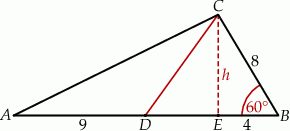
Jeżeli 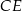 jest wysokością trójkąta
jest wysokością trójkąta 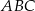 opuszczoną na bok
opuszczoną na bok 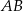 , to trójkąt
, to trójkąt 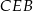 jest połówką trójkąta równobocznego o boku
jest połówką trójkąta równobocznego o boku 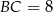 . W takim razie
. W takim razie
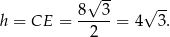
Ponadto wiemy, że 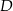 jest środkiem boku
jest środkiem boku 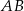 , więc
, więc
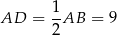
i pole trójkąta 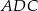 jest równe
jest równe
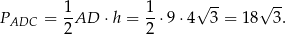
Odpowiedź: