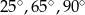/Szkoła podstawowa/Geometria/Trójkąt/Dowolny

Zadanie nr 2183366

Dodaj do ulubionych
Dodaj do rozwiązanych

Środkowa 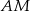AM trójkąta 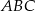ABC ma długość równą połowie długości boku 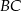BC . Miara kąta między tą środkową a wysokością 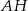AH jest równa 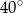40∘ . Wyznacz miary kątów trójkąta ABC .

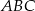Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

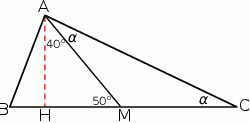
Sposób I

W trójkącie prostokątnym 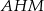AHM mamy

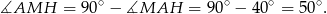
∡AMH = 90∘ − ∡MAH = 90∘ − 40∘ = 5 0∘.

Zauważmy teraz, że

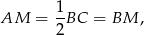
1 AM = -BC = BM , 2

co oznacza, że trójkąt 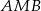AMB jest równoramienny. W takim razie

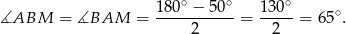
180∘ − 50∘ 130∘ ∡ABM = ∡BAM = -----------= -----= 65∘. 2 2

Zauważmy teraz, że trójkąt 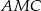AMC też jest równoramienny, więc możemy oznaczyć 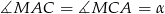∡MAC = ∡MCA = α . Korzystamy teraz z sumy kątów w trójkącie ABC .

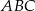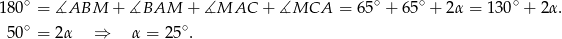
180∘ = ∡ABM + ∡BAM + ∡MAC + ∡MCA = 65∘ + 65∘ + 2α = 130∘ + 2α. ∘ ∘ 50 = 2 α ⇒ α = 2 5 .

Stąd

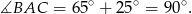
∘ ∘ ∘ ∡BAC = 65 + 25 = 90 .

Sposób II

Zauważmy, że równość 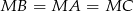MB = MA = MC oznacza, że punkty 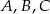A ,B ,C leżą na okręgu o środku 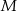M i średnicy 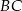BC . To oznacza, że trójkąt 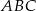ABC jest prostokątny i 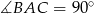∘ ∡BAC = 90 . Podobnie jak w poprzednim sposobie zauważamy, że

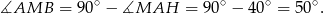
∘ ∘ ∘ ∘ ∡AMB = 9 0 − ∡MAH = 90 − 40 = 50 .

Teraz korzystamy z twierdzenia o kątach wpisanym i środkowym opartych na tym samym łuku.

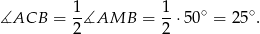
∡ACB = 1-∡AMB = 1-⋅5 0∘ = 25∘. 2 2

Stąd

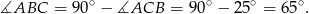
∡ABC = 90∘ − ∡ACB = 90∘ − 25∘ = 65∘ .

 
Odpowiedź: 25∘,6 5∘,90∘

Wersja PDF