Zadanie nr 3177175
Na środkowej 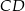 trójkąta
trójkąta 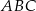 wybrano punkt
wybrano punkt 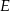 . Wykaż, że trójkąty
. Wykaż, że trójkąty 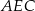 i
i 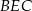 mają równe pola.
mają równe pola.
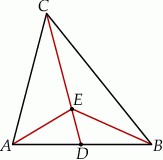
Rozwiązanie
Zauważmy, że trójkąty 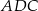 i
i 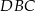 mają podstawy tej samej długości (
mają podstawy tej samej długości (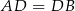 ) oraz wspólną wysokość opuszczoną na tę podstawę.
) oraz wspólną wysokość opuszczoną na tę podstawę.
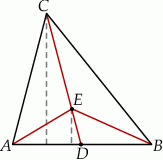
To oznacza, że trójkąty te mają równe pola
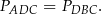
Podobnie, trójkąty 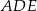 i
i 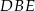 mają podstawy tej samej długości (
mają podstawy tej samej długości (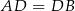 ) oraz wspólną wysokość opuszczoną z wierzchołka
) oraz wspólną wysokość opuszczoną z wierzchołka 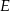 . Mają więc równe pola
. Mają więc równe pola
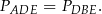
Mamy zatem