/Szkoła podstawowa/Geometria/Trójkąt/Dowolny

Zadanie nr 4616906

Dodaj do ulubionych
Dodaj do rozwiązanych

Na dwusiecznej 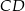CD trójkąta 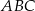ABC , w którym 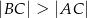|BC | > |AC | wybrano punkt 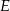E . Wykaż, że pole trójkąta 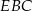EBC jest większe od pola trójkąta AEC .

PIC

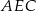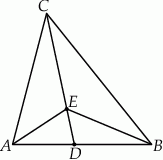
Rozwiązanie

Sposób I

Przypomnijmy, że dwusieczna dzieli kąt przy wierzchołku C na dwie równe części.

PIC

Korzystając ze wzoru z sinusem na pole trójkąta oraz z założenia 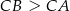CB > CA mamy

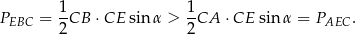
1- 1- PEBC = 2CB ⋅CE sin α > 2 CA ⋅ CE sinα = PAEC .

Sposób II

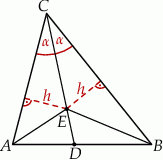
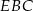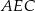Tym razem skorzystamy z tego, że każdy punkt dwusiecznej jest równoodległy od ramion kąta. To oznacza, że wysokości trójkątów EBC i AEC opuszczone z wierzchołka 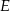E mają tę samą długość 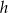h . Mamy zatem

1 1 PEBC = --⋅BC ⋅h > -AC ⋅h = PAEC . 2 2
Wersja PDF