Zadanie nr 6599525
Na boku 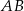 trójkąta
trójkąta 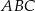 wybrano punkt
wybrano punkt 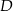 w ten sposób, że odległości punktów
w ten sposób, że odległości punktów 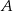 i
i 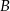 od prostej
od prostej 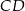 są równe (zobacz rysunek). Wykaż, że trójkąty
są równe (zobacz rysunek). Wykaż, że trójkąty 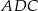 i
i 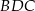 mają równe pola.
mają równe pola.
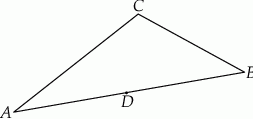
Rozwiązanie
Dorysujmy prostą 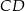 oraz rzuty punktów
oraz rzuty punktów 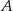 i
i 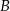 na tę prostą.
na tę prostą.
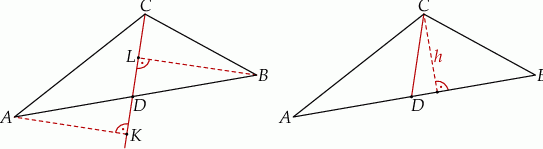
Sposób I
Zauważmy, że
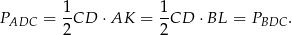
Sposób II
Zauważmy, że trójkąty prostokątne 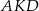 i
i 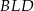 mają równe kąty przy wierzchołku
mają równe kąty przy wierzchołku 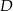 oraz przeciwprostokątne równej długości:
oraz przeciwprostokątne równej długości: 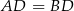 . To oznacza, że są one przystające i
. To oznacza, że są one przystające i 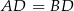 . Teraz wystarczy zauważyć, że trójkąty
. Teraz wystarczy zauważyć, że trójkąty 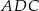 i
i 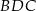 mają podstawy tej samej długości oraz wspólną wysokość opuszczoną z wierzchołka
mają podstawy tej samej długości oraz wspólną wysokość opuszczoną z wierzchołka 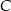 :
: