Zadanie nr 1340877
Przekątne czworokąta 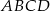 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 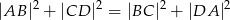 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
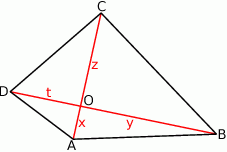
Niech 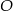 będzie punktem przecięcia się przekątnych i oznaczmy
będzie punktem przecięcia się przekątnych i oznaczmy 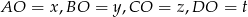 . Na mocy twierdzenia Pitagorasa mamy
. Na mocy twierdzenia Pitagorasa mamy
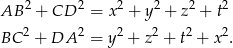
Zatem rzeczywiście 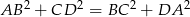 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przekątne czworokąta 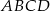 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 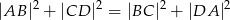 .
.
Rozpoczynamy od rysunku.

Niech 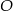 będzie punktem przecięcia się przekątnych i oznaczmy
będzie punktem przecięcia się przekątnych i oznaczmy 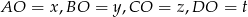 . Na mocy twierdzenia Pitagorasa mamy
. Na mocy twierdzenia Pitagorasa mamy
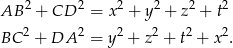
Zatem rzeczywiście 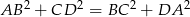 .
.
