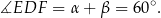/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny

Zadanie nr 1471587

Dodaj do ulubionych
Dodaj do rozwiązanych

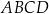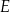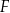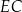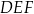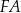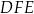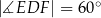Przeciwległe boki czworokąta ABCD wpisanego w okrąg przecinają się w punktach E i F (zobacz rysunek), przy czym odcinek EC jest zawarty w dwusiecznej kąta DEF , a odcinek FA jest zawarty w dwusiecznej kąta DF E . Wykaż, że |∡EDF | = 6 0∘ .

ZINFO-FIGURE

Rozwiązanie

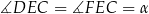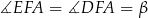Jeżeli oznaczymy ∡DEC = ∡F EC = α i ∡EFA = ∡DFA = β , to w trójkącie 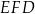EF D mamy

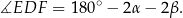
∡EDF = 180∘ − 2α − 2β.

Z drugiej strony, czworokąt ABCD jest wpisany w okrąg, więc

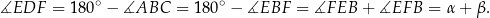
∘ ∘ ∡EDF = 180 − ∡ABC = 180 − ∡EBF = ∡F EB + ∡EF B = α+ β.

Zatem

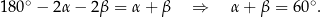
∘ ∘ 180 − 2α − 2β = α + β ⇒ α+ β = 60 .

Stąd

∡EDF = α+ β = 60∘.
Wersja PDF