Zadanie nr 2991192
W trójkącie 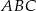 kąt wewnętrzny przy wierzchołku
kąt wewnętrzny przy wierzchołku 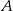 ma miarę
ma miarę 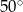 , a kąt wewnętrzny przy wierzchołku
, a kąt wewnętrzny przy wierzchołku 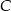 ma miarę
ma miarę 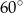 . Okrąg
. Okrąg 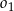 przechodzi przez punkt
przechodzi przez punkt 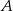 i przecina boki
i przecina boki 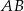 i
i 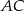 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 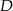 i
i 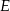 . Okrąg
. Okrąg 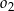 przechodzi przez punkt
przechodzi przez punkt 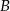 , przecina okrąg
, przecina okrąg 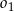 w punkcie
w punkcie 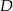 oraz w punkcie
oraz w punkcie 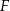 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 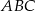 . Ponadto okrąg
. Ponadto okrąg 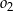 przecina bok
przecina bok 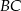 trójkąta w punkcie
trójkąta w punkcie 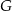 .
.
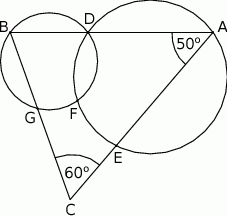
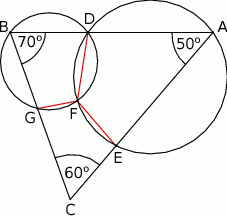
Udowodnij, że na czworokącie 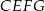 można opisać okrąg.
można opisać okrąg.
Rozwiązanie
Połączmy punkt 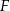 z punktami
z punktami 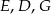 .
.
Z trójkąta 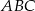 mamy
mamy
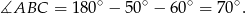
Wiemy ponadto, że na czworokątach 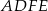 i
i 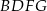 można opisać okręgi, więc
można opisać okręgi, więc
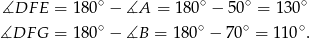
Stąd
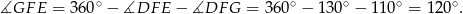
To oznacza, że
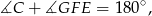
czyli na czworokącie 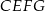 można opisać okrąg.
można opisać okrąg.

