Zadanie nr 3305838
Dany jest czworokąt wypukły 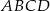 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 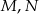 są odpowiednio środkami boków
są odpowiednio środkami boków 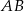 i
i 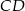 . Punkty
. Punkty 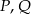 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 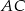 i
i 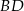 . Uzasadnij, że jeżeli odcinki
. Uzasadnij, że jeżeli odcinki 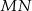 i
i 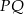 są prostopadłe, to
są prostopadłe, to 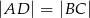 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
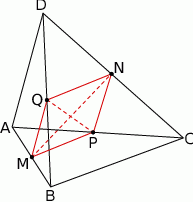
Sposób I
Zauważmy, że odcinek 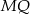 łączy środki boków w trójkącie
łączy środki boków w trójkącie 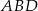 . Jest on więc równoległy do odcinka
. Jest on więc równoległy do odcinka 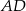 . Podobnie, odcinek
. Podobnie, odcinek 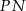 łączy środki boków trójkąta
łączy środki boków trójkąta 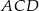 , więc też jest równoległy do
, więc też jest równoległy do 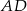 . Zatem
. Zatem

Analogicznie, jeżeli popatrzymy na trójkąty 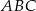 i
i 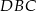 to
to

Ponadto
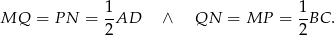
To oznacza, że czworokąt 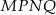 jest równoległobokiem. Z założenia wiemy ponadto, że jego przekątne są prostopadłe, więc jest to romb. W takim razie
jest równoległobokiem. Z założenia wiemy ponadto, że jego przekątne są prostopadłe, więc jest to romb. W takim razie
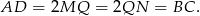
Sposób II
Umieśćmy czworokąt w układzie współrzędnych tak, aby 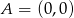 ,
, 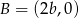 ,
, 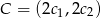 i
i 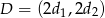 . Wtedy
. Wtedy
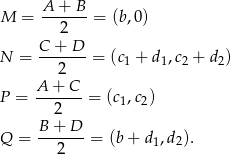
Obliczmy współrzędne wektorów 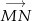 i
i 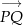 .
.
![−→ MN = [c + d − b,c + d ] 1 1 2 2 −→ PQ = [b + d1 − c1,d2 − c2].](https://img.zadania.info/zad/3305838/HzadR21x.gif)
Z założenia 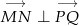 . Warunek ten najłatwiej jest zapisać używając iloczynu skalarnego – niezerowe wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy 0. Mamy zatem
. Warunek ten najłatwiej jest zapisać używając iloczynu skalarnego – niezerowe wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy 0. Mamy zatem
![−→ −→ 0 = MN ∘ PQ = [c1 + d1 − b,c2 + d2]∘ [b + d 1 − c1,d2 − c2] 0 = (d 1 + c1 − b)(d1 − (c1 − b))+ (d2 + c2)(d2 − c2) 0 = d 21 − (c1 − b)2 + d22 − c22 2 2 2 2 (c1 − b) + c2 = d1 + d2 / ⋅4 (2c − 2b)2 + (2c )2 = (2d )2 + (2d )2 1 2 1 2 BC 2 = AD 2.](https://img.zadania.info/zad/3305838/HzadR23x.gif)
Sposób III
Zauważmy, że
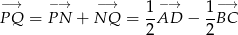
Podobnie,
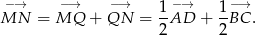
Z założenia 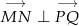 . Warunek ten najłatwiej jest zapisać używając iloczynu skalarnego – niezerowe wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy 0. Mamy zatem
. Warunek ten najłatwiej jest zapisać używając iloczynu skalarnego – niezerowe wektory są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy 0. Mamy zatem
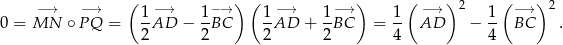
Ponieważ 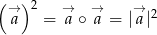 , mamy stąd
, mamy stąd
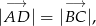
czyli w szczególności 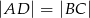 .
.

