/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny

Zadanie nr 4943885

Dodaj do ulubionych
Dodaj do rozwiązanych

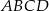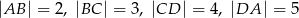Czworokąt ABCD jest wpisany w okrąg oraz |AB | = 2, |BC | = 3 , |CD | = 4, |DA | = 5 .

  • Oblicz co s∡BCD .
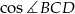  • Oblicz pole czworokąta ABCD .

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

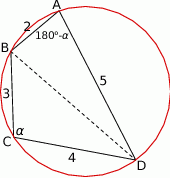
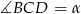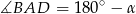Jeżeli oznaczymy ∡BCD = α to ∡BAD = 18 0∘ − α (własność czworokąta wpisanego w okrąg).

  • Napiszmy twierdzenia cosinusów w trójkątach 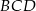BCD i BAD .
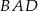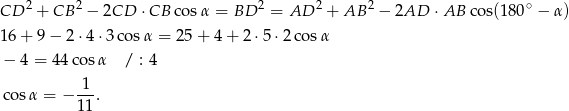
    CD 2 + CB 2 − 2CD ⋅CB cos α = BD 2 = AD 2 + AB 2 − 2AD ⋅AB cos(180∘ − α) 1 6+ 9 − 2 ⋅4 ⋅3co sα = 25+ 4+ 2⋅5 ⋅2 cosα − 4 = 44cos α / : 4 cosα = − -1-. 11

     
    Odpowiedź: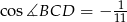 cos∡BCD = − 111

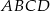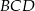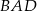  • Pole czworokąta ABCD liczymy jako sumę pól trójkątów BCD i BAD , które z kolei obliczmy korzystając ze wzoru sinusem. Zacznijmy od obliczenia sin α .
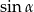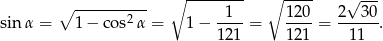
    ∘ -------- ∘ ---- √ --- ∘ -------2-- -1-- 1-20 2---30 sin α = 1− co s α = 1− 121 = 1 21 = 11 .

    Liczymy pole

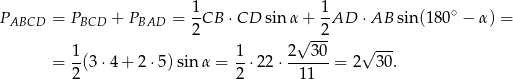
    1 1 PABCD = PBCD + PBAD = -CB ⋅CD sin α + --AD ⋅AB sin (180∘ − α) = 2 √ -2- 1- 1- 2--30- √ --- = 2 (3⋅4 + 2 ⋅5) sin α = 2 ⋅ 22⋅ 11 = 2 30.

     
    Odpowiedź: √ --- 2 30

Wersja PDF