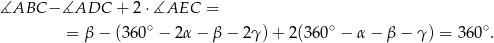Zadanie nr 6043486
Dwusieczne kątów 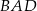 i
i 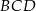 czworokąta wypukłego
czworokąta wypukłego 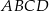 przecinają się w punkcie
przecinają się w punkcie 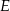 , przy czym punkty
, przy czym punkty 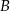 i
i 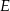 leżą po przeciwnych stronach prostej
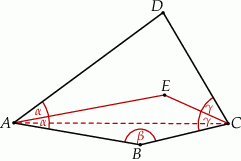
leżą po przeciwnych stronach prostej 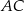 (zobacz rysunek).
(zobacz rysunek).
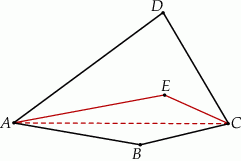
Wykaż, że 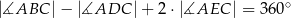 .
.
Rozwiązanie
Oznaczmy 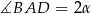 ,
, 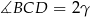 i
i 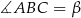 .
.
Z czworokąta 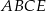 mamy
mamy
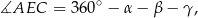
a z czworokąta 
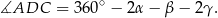
Zatem