/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny

Zadanie nr 6669961

Dodaj do ulubionych
Dodaj do rozwiązanych

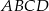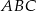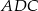Czworokąt ABCD jest wpisany w okrąg oraz pola trójkątów ABC i ADC są równe. Wykaż, że

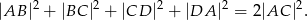
|AB |2 + |BC |2 + |CD |2 + |DA |2 = 2|AC |2.

Rozwiązanie

Oznaczmy 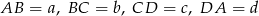AB = a, BC = b, CD = c, DA = d i ∡ABC = α .

PIC

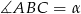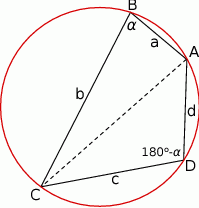
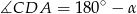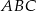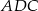Czworokąt jest wpisany w okrąg, więc ∡CDA = 1 80∘ − α . Spróbujmy najpierw rozszyfrować podaną informację o równości pól trójkątów ABC i ADC . Korzystamy ze wzoru na pole trójkąta z sinusem.

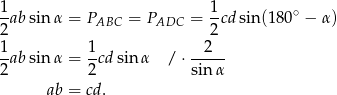
1- 1- ∘ 2ab sinα = PABC = PADC = 2cd sin (180 − α) 1 1 2 -ab sinα = -cd sinα / ⋅----- 2 2 sinα ab = cd.

Piszemy teraz twierdzenia cosinusów w trójkątach 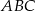ABC i ADC .

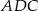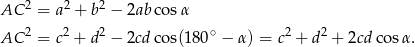
AC 2 = a2 + b2 − 2ab cosα 2 2 2 ∘ 2 2 AC = c + d − 2cd cos(180 − α) = c + d + 2cd cosα .

Dodajemy te równości stronami i mamy

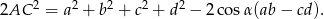
2 2 2 2 2 2AC = a + b + c + d − 2co sα(ab − cd ).

Jak zauważyliśmy wcześniej 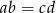ab = cd , więc mamy

2AC 2 = a2 + b2 + c2 + d2 = AB 2 + BC 2 + CD 2 + DA 2.
Wersja PDF