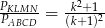Zadanie nr 7129799
Na bokach 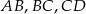 i
i 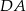 czworokąta
czworokąta 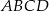 wybrano punkty
wybrano punkty 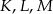 i
i 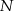 takie, że
takie, że
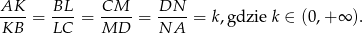
Oblicz stosunek pola czworokąta 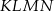 do pola czworokąta
do pola czworokąta 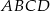 .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
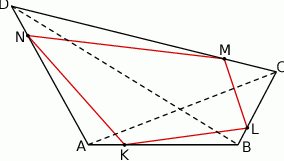
Pole czworokąta 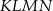 obliczmy odejmując od pola czworokąta
obliczmy odejmując od pola czworokąta 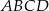 pola trójkątów
pola trójkątów 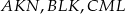 i
i  . Zauważmy najpierw, że z założenia
. Zauważmy najpierw, że z założenia 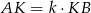 , więc
, więc
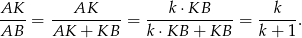
Podobnie
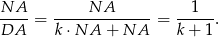
Korzystamy teraz ze wzoru na pole trójkąta z sinusem.
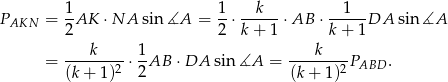
Analogicznie obliczamy
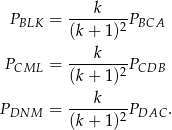
Mamy zatem
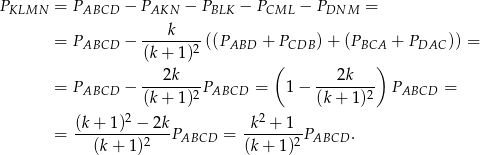
Zatem
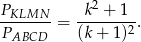
Odpowiedź: