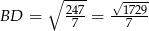/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny

Zadanie nr 7705491

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków czworokąta 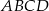ABCD są równe: 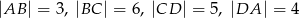|AB | = 3, |BC | = 6 , |CD | = 5, |DA | = 4 . Na czworokącie 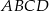ABCD opisano okrąg. Oblicz długość przekątnej 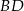BD tego czworokąta.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

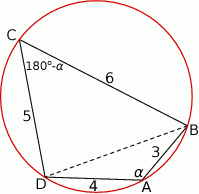
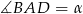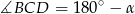Jeżeli oznaczymy ∡BAD = α to ∡BCD = 18 0∘ − α (własność czworokąta wpisanego w okrąg). Aby obliczyć 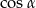co sα piszemy twierdzenia cosinusów w trójkątach 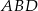ABD i BCD .

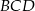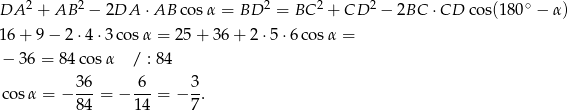
DA 2 + AB 2 − 2DA ⋅AB cosα = BD 2 = BC 2 + CD 2 − 2BC ⋅CD cos(180 ∘ − α ) 16 + 9− 2⋅ 4⋅3 cosα = 25 + 36 + 2 ⋅5⋅ 6cos α = − 36 = 84 cosα / : 84 3 6 6 3 cos α = − --- = − ---= − -. 8 4 14 7

Raz jeszcze piszemy twierdzenie cosinusów w trójkącie 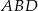ABD .

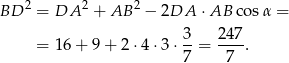
BD 2 = DA 2 + AB 2 − 2DA ⋅AB co sα = 3 247 = 16+ 9+ 2⋅4 ⋅3 ⋅--= ----. 7 7

Zatem 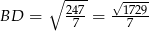---- ∘ 247 √-1729- BD = 7 = 7 .  
Odpowiedź: ∘ ---- 247 √1729 BD = 7 = 7

Wersja PDF