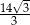Zadanie nr 7789063
Na czworokącie  można opisać okrąg. Długości boków tego czworokąta są równe
można opisać okrąg. Długości boków tego czworokąta są równe 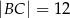 ,
, 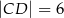 ,
, 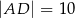 , a kąt
, a kąt 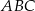 ma miarę
ma miarę 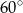 . Oblicz długość promienia okręgu opisanego na czworokącie
. Oblicz długość promienia okręgu opisanego na czworokącie 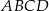 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
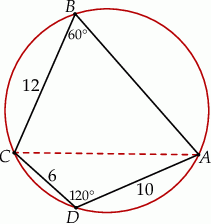
Ponieważ czworokąt 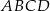 jest wpisany w okrąg, więc
jest wpisany w okrąg, więc
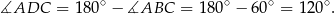
Korzystamy teraz z twierdzenia cosinusów w trójkącie 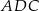 , aby obliczyć długość przekątnej
, aby obliczyć długość przekątnej 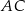
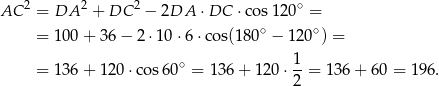
Stąd 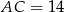 i na mocy twierdzenia sinusów interesujący na promień
i na mocy twierdzenia sinusów interesujący na promień 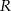 okręgu opisanego na czworokącie
okręgu opisanego na czworokącie  (a więc też na trójkącie
(a więc też na trójkącie  ) spełnia warunek
) spełnia warunek
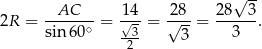
Stąd 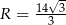 .
.
Odpowiedź: