/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny

Zadanie nr 9621249

Dodaj do ulubionych
Dodaj do rozwiązanych

Czworokąt 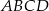ABCD jest wpisany w okrąg. Dane są 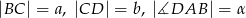|BC | = a, |CD | = b, |∡DAB | = α . Wyznacz długość przekątnej BD .

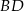Rozwiązanie

Rozpoczynamy od rysunku.

PIC

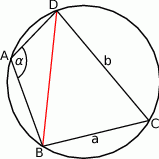
Ponieważ sumy przeciwległych kątów czworokąta wpisanego w okrąg są równe 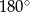18 0∘ , mamy

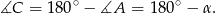
∡C = 180∘ − ∡A = 180∘ − α.

Możemy więc wyliczyć długość przekątnej 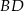BD korzystając z twierdzenia cosinusów w trójkącie BCD .

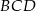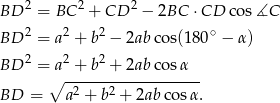
BD 2 = BC 2 + CD 2 − 2BC ⋅CD cos ∡C 2 2 2 ∘ BD = a + b − 2ab cos(180 − α ) BD 2 = a2 + b2 + 2ab cosα ∘ ------------------- BD = a2 + b2 + 2ab cos α.

 
Odpowiedź: √ -2----2------------ BD = a + b + 2ab cos α

Wersja PDF