Zadanie nr 1069921
Okrąg przecina boki czworokąta 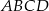 kolejno w punktach
kolejno w punktach 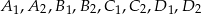 (zobacz rysunek).
(zobacz rysunek).
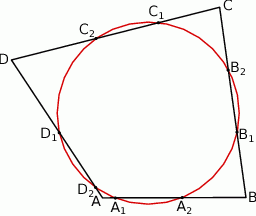
Wykaż, że jeżeli 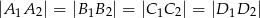 , to w czworokąt
, to w czworokąt 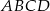 można wpisać okrąg.
można wpisać okrąg.
Rozwiązanie
Sposób I
Niech  będzie promieniem danego okręgu i
będzie promieniem danego okręgu i
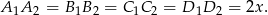
Oznaczmy ponadto przez 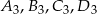 rzuty środka okręgu na kolejne boki czworokąta.
rzuty środka okręgu na kolejne boki czworokąta.
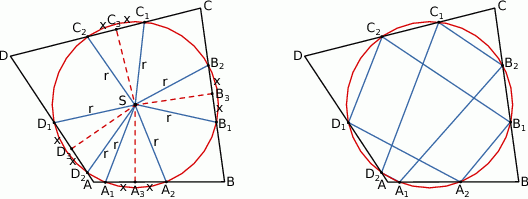
Zauważmy, że cztery trójkąty równoramienne
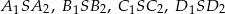
są przystające (bo mają boki równej długości), więc
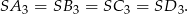
To z kolei oznacza, że okrąg o środku 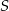 i promieniu
i promieniu 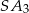 jest styczny do wszystkich boków czworokąta.
jest styczny do wszystkich boków czworokąta.
Sposób II
Popatrzmy na proste 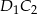 i
i 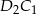 . Odcinają one od danego okręgu łuki
. Odcinają one od danego okręgu łuki 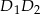 i
i 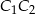 , które są tej samej długości. Proste te są więc równoległe i czworokąt
, które są tej samej długości. Proste te są więc równoległe i czworokąt 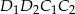 jest trapezem równoramiennym. W szczególności
jest trapezem równoramiennym. W szczególności
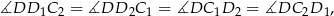
czyli trójkąt 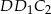 jest równoramienny. Zatem
jest równoramienny. Zatem 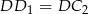 .
.
Analogicznie uzasadniamy, że każdy z czworokątów 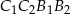 ,
, 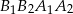 i
i 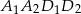 jest trapezem równoramiennym i
jest trapezem równoramiennym i 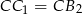 ,
, 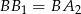 ,
, 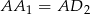 . Stąd
. Stąd
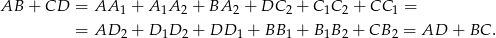
To oczywiście oznacza, że w czworokąt 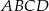 można wpisać okrąg.
można wpisać okrąg.

