Zadanie nr 1855653
W czworokącie wypukłym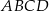 
poprowadzono przekątną 
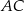. Okręgi wpisane w trójkąty 
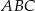i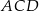 
są styczne zewnętrznie. Wykaż, że w czworokąt 
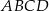można wpisać okrąg.
Rozwiązanie
Szkicujemy opisaną sytuację.
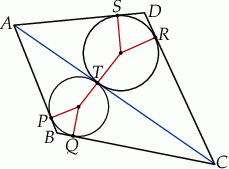
Korzystamy z tego, że odcinki stycznych poprowadzonych do okręgu z punktu znajdującego się na zewnątrz tego okręgu mają równe długości.
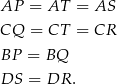
Mamy zatem
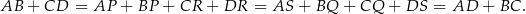
To oznacza, że w czworokąt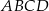 
rzeczywiście można wpisać okrąg.
