Zadanie nr 1937464
Przekątne czworokąta 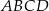 wpisanego w okrąg przecinają się w punkcie
wpisanego w okrąg przecinają się w punkcie 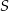 , a punkt
, a punkt 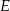 jest takim punktem przekątnej
jest takim punktem przekątnej 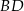 , że
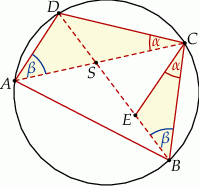
, że 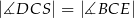 (zobacz rysunek).
(zobacz rysunek).
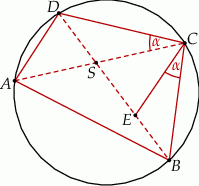
Wykaż, że 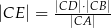 .
.
Rozwiązanie
Zauważmy, że 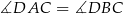 (kąty wpisane oparte na tym samym łuku).
(kąty wpisane oparte na tym samym łuku).
W takim razie trójkąty 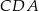 i
i 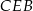 mają dwa równe kąty, więc są podobne. Stąd
mają dwa równe kąty, więc są podobne. Stąd