Zadanie nr 2926623
Wykaż, że jeżeli każda przekątna czworokąta wypukłego dzieli go na trójkąty o równych polach to czworokąt ten jest równoległobokiem.
Rozwiązanie
Szkicujemy czworokąt.
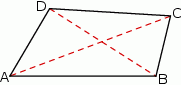
Zauważmy, że jeżeli trójkąty 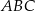 i
i 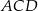 mają równe pola, to pole każdego z nich jest równe połowie pola czworokąta. Tak samo uzasadniamy, że pola trójkątów
mają równe pola, to pole każdego z nich jest równe połowie pola czworokąta. Tak samo uzasadniamy, że pola trójkątów 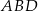 i
i 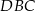 są równe połowie pola czworokąta. W szczególności
są równe połowie pola czworokąta. W szczególności
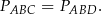
Trójkąty te mają wspólną podstawę 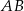 , więc muszą mieć wysokości tej samej długości, czyli punkty
, więc muszą mieć wysokości tej samej długości, czyli punkty 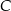 i
i 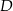 leżą w tej samej odległości od prostej
leżą w tej samej odległości od prostej 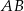 , czyli proste
, czyli proste 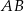 i
i 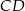 są równoległe.
są równoległe.
Analogicznie z, z równości pól 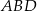 i
i 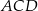 uzasadniamy, że równoległe są proste
uzasadniamy, że równoległe są proste 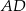 i
i 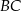 . To oznacza, że czworokąt
. To oznacza, że czworokąt 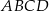 jest równoległobokiem.
jest równoległobokiem.

