Zadanie nr 3242379
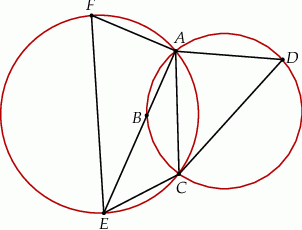
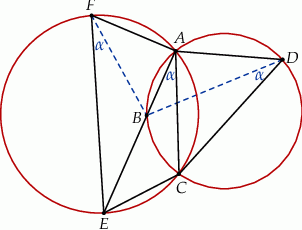
Czworokąt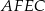 
jest wpisany w okrąg i jego przekątna 
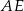przecina okrąg opisany na trójkącie 
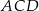w punkcie 
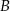(zobacz rysunek).
Zachodzi ponadto równość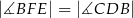 
. Udowodnij, że punkty 
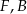i 
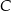są współliniowe.
Rozwiązanie
Dorysujmy odcink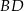i 
i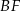 
.
Jeżeli oznaczymy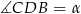 
, to również
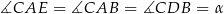
(jako kąty wpisane oparte na tych samych łukach). Z tego samego powodu
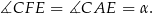
Ale z założenia również
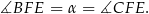
To oznacza, że rzeczywiście punkt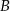 
leży na odcinku 
.
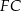