Zadanie nr 5128574
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
- Jeśli środki boków czworokąta wyznaczają prostokąt, czy można stwierdzić, że czworokąt jest rombem?
- Jeśli środki boków czworokąta wyznaczają romb, czy można stwierdzić, że czworokąt jest prostokątem?
- Jeśli środki boków czworokąta wyznaczają kwadrat, czy można stwierdzić, że czworokąt jest kwadratem?
Rozwiązanie
Zacznijmy od rysunku.
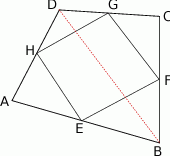
Jeżeli dorysujemy przekątną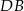 
, to na mocy wierdzenia Talesa jest ona równoległa do odcinków 
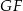i 
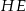. Podobnie, odcink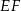i 
i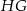 
są równoległe do przekątnej 
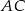. Czworokąt 
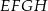jest więc równoległobokiem. Zauważmy ponadto, że boki tego równoległoboku mają długości równe połowom długuści przekątnych wyjściowego czworokąta.
- Czworokąt
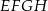jest prostokątem, wtedy i tylko wtedy gdy przekątne 
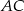i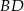 
są prostopadłe. Jest wiele czworokątów o tej własności, które nie są rombami, np. deltoid (rysunek).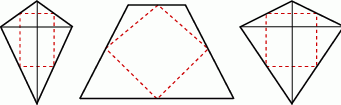 
Odpowiedź: Nie - Czworokąt
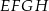jest rombem, wtedy i tylko wtedy gdy przekątne 
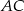i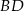 
mają równe długości. Jest wiele czworokątów o tej własności, które nie są prostokątami, np. trapez równoramienny (rysunek).
Odpowiedź: Nie - Czworokąt
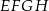jest kwadratem, wtedy i tylko wtedy gdy przekątne 
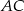i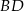 
są prostopadłe i mają równe długości. Jest wiele czworokątów o tej własności, które nie są prostokątami, np. deltoid z równymi przekątnymi (rysunek).
Odpowiedź: Nie
