Zadanie nr 7605277
Dwa przeciwległe boki czworokąta wpisanego w okrąg mają równe długości. Wykaż, że czworokąt ten jest trapezem.
Rozwiązanie
Rozpoczynamy od rysunku.
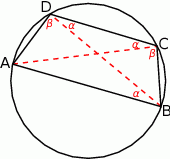
Niech 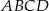 będzie czworokątem wpisanym w okrąg i niech
będzie czworokątem wpisanym w okrąg i niech 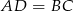 .
.
Sposób I
Zauważmy, że
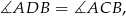
bo kąty te są oparte na tym samym łuku. Podobnie
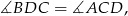
bo kąty te są oparte na łukach tej samej długości (tu korzystamy z tego, że 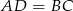 ). W takim razie
). W takim razie 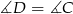 . Ponieważ sumy przeciwległych kątów w czworokącie wpisanym w okrąg są równe
. Ponieważ sumy przeciwległych kątów w czworokącie wpisanym w okrąg są równe 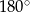 , mamy
, mamy
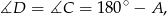
a to oznacza, że proste 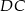 i
i 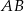 przecinają prostą
przecinają prostą 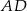 pod tym samym kątem, więc są równoległe.
pod tym samym kątem, więc są równoległe.
Sposób II
Tak jak poprzednio zauważamy, że
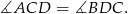
Zauważmy ponadto, że
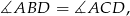
jako kąty oparte na tym samym łuku. To oznacza, że proste 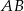 i
i 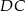 przecinają przekątną
przecinają przekątną 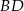 pod tym samym kątem, więc są równoległe.
pod tym samym kątem, więc są równoległe.

