/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Udowodnij...

Zadanie nr 7972113

Przekątne czworokąta wypukłego 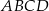ABCD dzielą go na cztery trójkąty. Wykaż, że jeżeli promienie okręgów opisanych na tych czterech trójkątach są równe, to w czworokąt 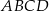ABCD można wpisać okrąg.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

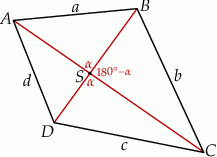
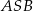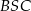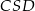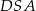Informację o równych promieniach okręgów opisanych na trójkątach ASB , BSC , CSD i DSA najłatwiej zapisać przy użyciu twierdzenia sinusów.

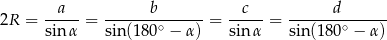
--a-- ------b------- --c-- ------d------- 2R = sin α = sin (180∘ − α) = sin α = sin(180∘ − α)

Ponieważ

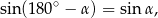
sin(180∘ − α ) = sin α,

mamy stąd

a = b = c = d ,

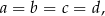
czyli czworokąt 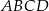ABCD jest rombem. W szczególności można w ten czworokąt wpisać okrąg – jego środkiem jest punkt przecięcia się przekątnych.

PIC

Wersja PDF