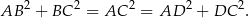Zadanie nr 8863014
Przekątna 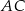 czworokąta
czworokąta 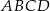 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 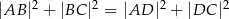 .
.
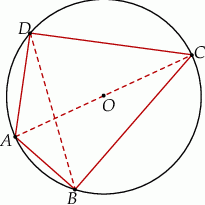
Rozwiązanie
Zauważmy, że trójkąty 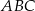 i
i 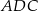 są prostokątne (bo kąty oparte na średnicy są proste). Mamy stąd
są prostokątne (bo kąty oparte na średnicy są proste). Mamy stąd
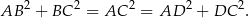
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przekątna 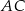 czworokąta
czworokąta 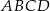 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 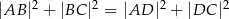 .
.

Zauważmy, że trójkąty 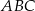 i
i 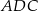 są prostokątne (bo kąty oparte na średnicy są proste). Mamy stąd
są prostokątne (bo kąty oparte na średnicy są proste). Mamy stąd