/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Udowodnij...

Zadanie nr 9127139

Z wierzchołków czworokąta 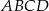ABCD poprowadzono półproste, które przecinają się w wierzchołkach czworokąta 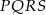PQRS wpisanego w okrąg (zobacz rysunek).

PIC

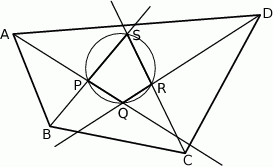
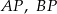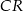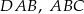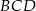Wykaż, że jeżeli półproste AP , BP i CR są dwusiecznymi odpowiednio kątów DAB , ABC i BCD , to półprosta 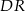DR jest dwusieczną kąta CDA .

Wersja PDF

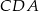Rozwiązanie

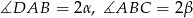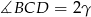Oznaczymy kąty czworokąta przez ∡DAB = 2α, ∡ABC = 2β i ∡BCD = 2γ .

PIC

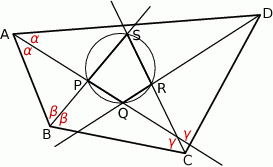
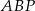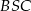Patrzymy najpierw na trójkąty ABP i BSC . Mamy w nich

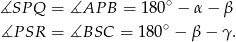
∘ ∡SP Q = ∡AP B = 180 − α − β ∡P SR = ∡BSC = 180∘ − β − γ .

Wiemy ponadto, że punkty 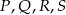P,Q ,R ,S leżą na jednym okręgu – to pozwala obliczyć pozostałe kąty czworokąta PQRS .

∡SRQ = 180∘ − ∡SP Q = 180∘ − (180∘ − α − β ) = α + β ∘ ∘ ∘ ∡P QR = 180 − ∡P SR = 1 80 − (180 − β − γ ) = β + γ.

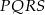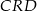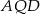Teraz z trójkątów CRD i AQD obliczamy miary kątów, na jakie prosta 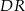DR dzieli kąt ADC .

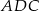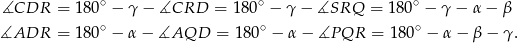
∡CDR = 180∘ − γ − ∡CRD = 1 80∘ − γ − ∡SRQ = 180∘ − γ − α − β ∡ADR = 180∘ − α − ∡AQD = 180∘ − α − ∡P QR = 180∘ − α − β − γ .

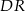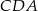Zatem rzeczywiście prosta DR jest dwusieczną kąta CDA .

Wersja PDF