Zadanie nr 8980675
Przekątna 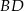 rombu
rombu 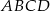 przecina jego wysokość
przecina jego wysokość 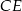 , poprowadzoną na bok
, poprowadzoną na bok 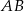 , w punkcie
, w punkcie 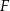 . Oblicz pole rombu
. Oblicz pole rombu 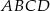 , jeśli wiadomo, że
, jeśli wiadomo, że 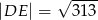 oraz
oraz 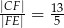 .
.
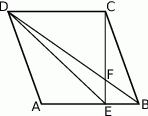
Rozwiązanie
Korzystając z podanego stosunku długości odcinków 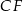 i
i 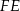 możemy oznaczyć ich długości przez
możemy oznaczyć ich długości przez 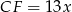 i
i 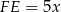 . Jeżeli ponadto oznaczymy długość boku rombu przez
. Jeżeli ponadto oznaczymy długość boku rombu przez 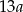 to z podobieństwa trójkątów
to z podobieństwa trójkątów 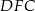 i
i 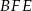 mamy
mamy
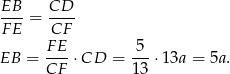
Potrzebujemy teraz dwóch równań wiążących ze sobą  i
i  – otrzymamy je pisząc twierdzenia Pitagorasa w trójkątach
– otrzymamy je pisząc twierdzenia Pitagorasa w trójkątach 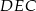 i
i 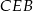 .
.
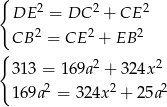
Odejmujemy od pierwszego równania drugie (żeby skrócić 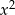 ) i mamy
) i mamy
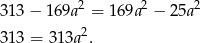
Zatem 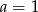 i z pierwszego równania mamy
i z pierwszego równania mamy
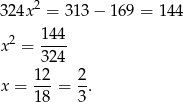
Teraz bez trudu liczymy pole rombu
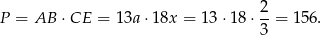
Odpowiedź: 156

