/Szkoła średnia/Nierówności/Udowodnij.../Kwadratowe

Zadanie nr 3457248

Dodaj do ulubionych
Dodaj do rozwiązanych

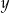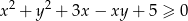Wykaż, że dla każdej liczby rzeczywistej x i dla każdej liczby rzeczywistej y prawdziwa jest nierówność x2 + y2 + 3x − xy + 5 ≥ 0 .

Rozwiązanie

Sposób I

Przekształcamy daną nierówność w sposób równoważny.

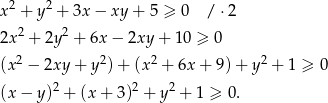
2 2 x + y + 3x− xy + 5 ≥ 0 / ⋅2 2x2 + 2y2 + 6x − 2xy + 1 0 ≥ 0 2 2 2 2 (x − 2xy + y ) + (x + 6x + 9) + y + 1 ≥ 0 (x− y)2 + (x+ 3)2 + y 2 + 1 ≥ 0.

Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność też musiała być spełniona.

Sposób II

Potraktujmy nierówność

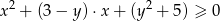
2 2 x + (3− y)⋅ x+ (y + 5) ≥ 0

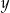jak nierówność kwadratową zmiennej x z parametrem y . Współczynnik przy 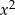x2 jest dodatni, więc wykresem lewej strony nierówności (dla ustalonego 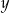y –ka) jest parabola o ramionach skierowanych w górę. Wystarczy zatem wykazać, że parabola ta nigdy nie przecina osi 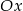Ox , czyli, że Δ < 0 .

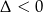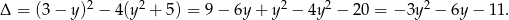
Δ = (3 − y)2 − 4(y2 + 5) = 9 − 6y + y2 − 4y 2 − 20 = − 3y2 − 6y − 11.

Wykresem otrzymanego wyrażenia jest parabola o ramionach skierowanych w dół oraz

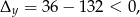
Δy = 36 − 13 2 < 0,

więc rzeczywiście zawsze 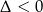Δ < 0 . To oznacza, że dana nierówność jest spełniona dla wszystkich możliwych wartości x i y .

Sposób III

Przekształcamy daną nierówność w sposób równoważny.

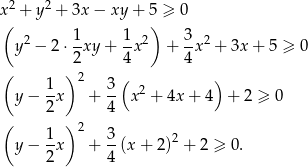
2 2 x + y + 3x − xy + 5 ≥ 0 ( 1 1 ) 3 y2 − 2⋅ -xy + -x2 + -x 2 + 3x + 5 ≥ 0 2 4 4 ( 1 ) 2 3( ) y − --x + -- x2 + 4x + 4 + 2 ≥ 0 2 4 ( 1 ) 2 3 2 y − --x + -(x + 2) + 2 ≥ 0 . 2 4

Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność też musiała być spełniona.

Wersja PDF