Zadanie nr 4160642
Wykaż, że dla dowolnych liczb rzeczywistych 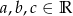 zachodzi nierówność
zachodzi nierówność
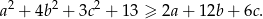
Rozwiązanie
Przekształcamy nierówność tak, aby otrzymać z lewej strony nierówności sumę kwadratów.
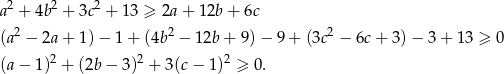
Teraz jest jasne, że nierówność ta jest zawsze spełniona.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla dowolnych liczb rzeczywistych 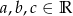 zachodzi nierówność
zachodzi nierówność
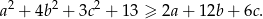
Przekształcamy nierówność tak, aby otrzymać z lewej strony nierówności sumę kwadratów.
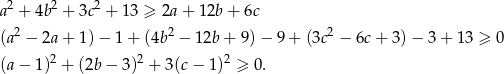
Teraz jest jasne, że nierówność ta jest zawsze spełniona.
